
Mit mehr als hundert Ausgaben unserer Rätselserie haben wir Sie unterhalten, ins Grübeln und womöglich sogar ins Schwitzen gebracht - intellektuell gesehen. Finden Sie hier eine Auswahl der beliebtesten Rätsel samt der von SZ.de-Lesern eingesandten Auflösungen Wie viele Punkte hat Schalke geholt? Bei einem Fußballturnier treten fünf Mannschaften an, jede spielt einmal gegen jede. Für einen Sieg gibt es zwei Punkte, bei einem Remis bekommen beide Mannschaften je einen Zähler. Nach sämtlichen Begegnungen sieht die Rangliste so aus: Wie viele Punkte muss Schalke demnach geholt haben? Die Lösung finden Sie auf der nächsten Seite.

Liebe Leser, wenngleich wir mit unserer - natürlich völlig frei erfundenen - Tabelle nicht alle Fan-Perspektiven zufriedenstellen konnten: gerätselt haben Sie wie immer sehr fleißig. Die Lösung der Aufgabe erklärt stellvertretend für viele Teilnehmer Lukas K.: "Für die Lösung ist die Anzahl der Siege und Unentschieden der einzelnen Mannschaften unerheblich, da bei jeder Partie genau zwei Punkte vergeben werden - entweder zwei für den Sieger, oder jeweils einen für jede Mannschaft bei einem Unentschieden. Bei fünf Mannschaften, die gegeneinander spielen, gibt es n*(n-1)/2 Partien, also 5*4/2 = 10. Somit werden 20 Punkte vergeben. Da die anderen Mannschaften zusammen 17 Punkte geholt haben, muss Schalke genau drei Punkte geholt haben." Beim nächsten Rätsel hängen Buchstaben und Ziffern zusammen.

Können Sie das Buchstabenrätsel entschlüsseln? In der Gleichung müssen Sie die Buchstaben so durch Ziffern ersetzen, dass die Rechnung aufgeht. Dabei darf jede Ziffer nur einmal verwendet werden, verschiedene Buchstaben entsprechen verschiedenen Ziffern und eine Zahl darf nicht mit Null beginnen. Ein Beispiel: Der Code I + BB = ILL hat die Lösung 1 + 99 = 100. Die Lösung finden Sie auf der nächsten Seite.

Ausnahmsweise ein Rätsel mit einer eindeutigen Lösung - wenigstens für die vielen Leser, die sich an sämtliche Vorgaben (siehe oben) gehalten haben. Daher wollen wir uns heute auch nicht mit Plaudereien aufhalten. Die korrekte Lösung samt Herleitung präsentiert Mitspieler Ulrich W.: "Aus zwei vierstelligen Zahlen kann nur eine fünfstellige mit einer 1 am Anfang werden. M ist also 1. X + 1 + [0,1] = 1Y hat für X nur die Lösung 8 oder 9, für Y nur 0 oder 1, wobei die 1 schon verbraucht ist. Also ist O 0. E + 0 + Überlauf = N ergibt, dass N = E + 1 und Überlauf an dritter Stelle 1 ist. N + R + Ü2 = 1E ergibt demnach R + Ü2 + 1 = 10, also auch R ist 8 oder 9. Demnach muss E kleiner als 7 sein und somit kann an der vierten Stelle kein Überlauf dazu kommen. S ist also 9, R ist 8. Ü2 muss dann zwingend 1 sein, also D + E = 1Y, wobei Y > 1 sein muss. Der Rest lässt sich kurz ausprobieren, dann hat man: 9567 + 1085 = 10652." Das nächste Rätsel führt uns zurück in die Antike.

Wie alt wurde Diophantos? Mal wieder ein Rätsel aus dem antiken Griechenland. Auf dem Grabstein des großen Mathematikers Diophantos von Alexandria soll angeblich das hier gestanden haben (wir vereinfachen das Original im Sinne der Verständlichkeit ein wenig): Diophantos' Jugend dauerte ein Sechstel seines Lebens; ein Lebenszwölftel später wuchs ihm ein Bart; ein weiteres Siebtel seines Lebens später heiratete er und hatte fünf Jahre danach einen Sohn; der Sohn lebte exakt halb so lang wie sein Vater und Diophantos verstarb vier Jahre nach dem Tod seines Kindes. Die Lösung finden Sie im nächsten Bild.

Auch Rätsel von anno dazumal können Sie offensichtlich nicht schocken, liebe Leser. Jedenfalls haben wir viele gut durchkalkulierte und fast ausschließlich korrekte Lösungen eingesandt bekommen. Wie man zum richtigen Ergebnis kommen konnte, erklärt stellvertretend Mitspieler Klaus S.: "Diophantos verstarb im Alter von 84 Jahren. In der Annahme, dass die genannten Lebensabschnitte in ganzen Jahren darstellbar sind, habe ich das kleinste gemeinsame Vielfache von sechs, zwölf und sieben bestimmt, das ist 84. Demnach bekam er seinen Sohn im Alter von 14 + 7 + 12 + 5 = 38 Jahren. Als dieser mit 84/2 = 42 Jahren starb, war Diophantos 38 + 42 = 80 Jahre alt." Natürlich lässt sich das Ganze auch als mathematische Formel darstellen, mit Diophantos' Alter als Variable x: x/6 + x/12 + x/7 + 5 + x/2 + 4 = x Beim nächsten Rätsel geht es um eine manchmal knifflige Alltagssituation.
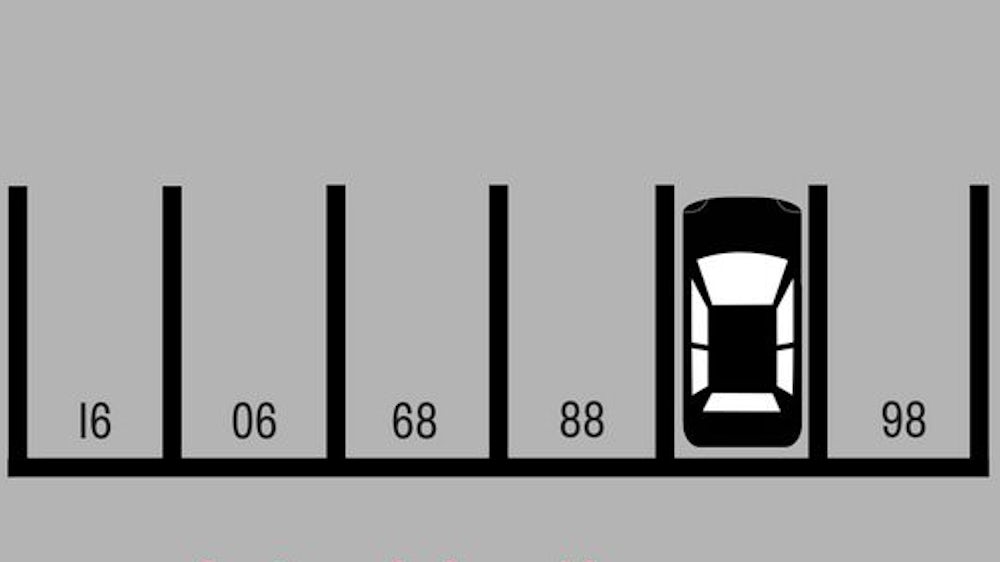
Wo parkt das Auto? Im Parkhaus: Anhand der sichtbaren Nummern müssen Sie herausbekommen, auf welchem Parkplatz der Wagen steht. Die Lösung finden Sie auf der nächsten Seite.

Liebe Leser, vielen Dank dafür, dass Sie die SZ offenbar für ein Qualitätsmedium halten, dessen Rätsel in jedem Fall maximal komplex sein müssen. So jedenfalls würden wir uns die vielen Einsendungen mit teils abenteuerlichen Zahlenspielen erklären, die wir für diese Aufgabe erhalten haben. Ein kleines Beispiel: "Der Wagen parkt auf Platz 58! 06 - 16 = -10 68 - 88 = - 20 98 - 58 = - 40 Verdopplung der Differenz!" Nein, leider nicht! Denn das Rätsel war diese Woche nicht maximal kompliziert, sondern maximal einfach - wenigstens aus dem richtigen Blickwinkel betrachtet. Denn wer das Handy/den Computerbildschirm/sich selbst kurz um 180 Grad gedreht hat, konnte sehen, was zum Beispiel Leser Bernhard S. gesehen hat: "Der Wagen parkt auf Nr. 87. Bei dem Bild handelt es sich um die Vogelperspektive eines Parkdecks, bei dem die Zahlen natürlich so angeordnet sind, dass der einparkende Autofahrer sie lesen kann. Aus unserer Perspektive stehen sie auf dem Kopf." Beim Rätsel im nächsten Bild geht es um Zahlen.

Wie lautet bloß die Zahl? Gesucht ist eine sechsstellige Zahl, die die drei Bedingungen aus dem Bild oben erfüllt. Die Lösung finden Sie auf der nächsten Seite.

Die Lösung Liebe Leser, viele von Ihnen sind mit Unterstützung von Excel und weiteren digitalen HIlfsmitteln auf die Lösung gekommen. Manche, wie zum Beispiel Klaus D., haben es aber auch mit ein wenig Kombinieren geschafft: "Die erste Ziffer musste kleiner als fünf, also eine Vier sein. Dann überschlagen Sie die Möglichkeiten zur Quersumme 43, es müssen hohe Ziffern vorkommen, also mehrere Neuner. Nun noch ein wenig kombinieren, siehe Quadrat, und schon kommt man auf 499849." Beim nächsten Rätsel geht es um Zeitmessung mithilfe von Sanduhren.

Wie messe ich Zeit mit der Sanduhr? Sie haben zwei Sanduhren. Den Sand einmal komplett durchrieseln zu lassen, dauert bei der einen sieben und bei der anderen elf Minuten. Wie können Sie mit den beiden Sanduhren exakt eine Viertelstunde messen? Die Lösung finden Sie im nächsten Bild.

Liebe Leser, bei dieser Knobelei führen viele Wege zum gewünschten Ergebnis. Der zeitsparendste funktioniert so (wir nennen die Sanduhren der Einfachheit halber S11 und S7): Beide Sanduhren umdrehen; sobald der komplette Sand in S7 durchgelaufen ist, sind sieben Minuten vergangen und in S11 muss noch Sand für weitere vier Minuten durchrieseln. S7 sofort wieder umdrehen und die verbleibenden vier Minuten von S11 abwarten; sobald dort der komplette Sand durchgelaufen ist - es sind nun insgesamt elf Minuten vergangen - befindet sich in S7 Sand für vier Minuten im unteren Teil der Sanduhr. S7 wieder umdrehen und den "Vier-Minuten-Sand" wieder zurücklaufen lassen - und schon ist eine Viertelstunde abgemessen. Noch nicht genug gerätselt? Hier finden Sie weitere bereits erschienene Ausgaben der Serie "Knobelei der Woche" - mit Lösungen!