
Das Rätsel der Woche Gesucht ist eine sechsstellige Zahl, die die drei Bedingungen aus dem Bild oben erfüllt. Die Lösung finden Sie auf der nächsten Seite.

Die Lösung Liebe Leser, viele von Ihnen sind mit Unterstützung von Excel und weiteren digitalen HIlfsmitteln auf die Lösung gekommen. Manche, wie zum Beispiel Klaus D., haben es aber auch mit ein wenig Kombinieren geschafft: "Die erste Ziffer musste kleiner als fünf, also eine Vier sein. Dann überschlagen Sie die Möglichkeiten zur Quersumme 43, es müssen hohe Ziffern vorkommen, also mehrere Neuner. Nun noch ein wenig kombinieren, siehe Quadrat, und schon kommt man auf 499849." Noch nicht genug gerätselt? Auf den folgenden Seiten finden Sie weitere Ausgaben unserer Knobelei der Woche.

Das Rätsel der Woche Sie haben zwei Sanduhren. Den Sand einmal komplett durchrieseln zu lassen, dauert bei der einen sieben und bei der anderen elf Minuten. Wie können Sie mit den beiden Sanduhren exakt eine Viertelstunde messen?

Die Lösung Liebe Leser, bei dieser Knobelei führen viele Wege zum gewünschten Ergebnis. Der zeitsparendste funktioniert so (wir nennen die Sanduhren der Einfachheit halber S11 und S7): Beide Sanduhren umdrehen; sobald der komplette Sand in S7 durchgelaufen ist, sind sieben Minuten vergangen und in S11 muss noch Sand für weitere vier Minuten durchrieseln. S7 sofort wieder umdrehen und die verbleibenden vier Minuten von S11 abwarten; sobald dort der komplette Sand durchgelaufen ist - es sind nun insgesamt elf Minuten vergangen - befindet sich in S7 Sand für vier Minuten im unteren Teil der Sanduhr. S7 wieder umdrehen und den "Vier-Minuten-Sand" wieder zurücklaufen lassen - und schon ist eine Viertelstunde abgemessen.

Das Rätsel der Woche Finden Sie eine fünfstellige Zahl, für die folgendes gilt: die erste Ziffer ist die Hälfte der vierten Ziffer; die zweite Ziffer ist ein Viertel der letzten Ziffer; die vierte Ziffer ist das Dreifache der zweiten Ziffer; die dritte Ziffer entspricht der ersten Ziffer plus vier.

Die Lösung Liebe Leser, diesmal war die Aufgabe zugegebenermaßen nicht allzu knifflig. Zumindest, wenn man die etwas kompliziert formulierte Angabe in vier Gleichungen übersetzt hat, dafür bezeichnen wir die Ziffern mit den Buchstaben a bis e: a = 0,5 * d b = 0,25 * e d = 3 * b c = a + 4
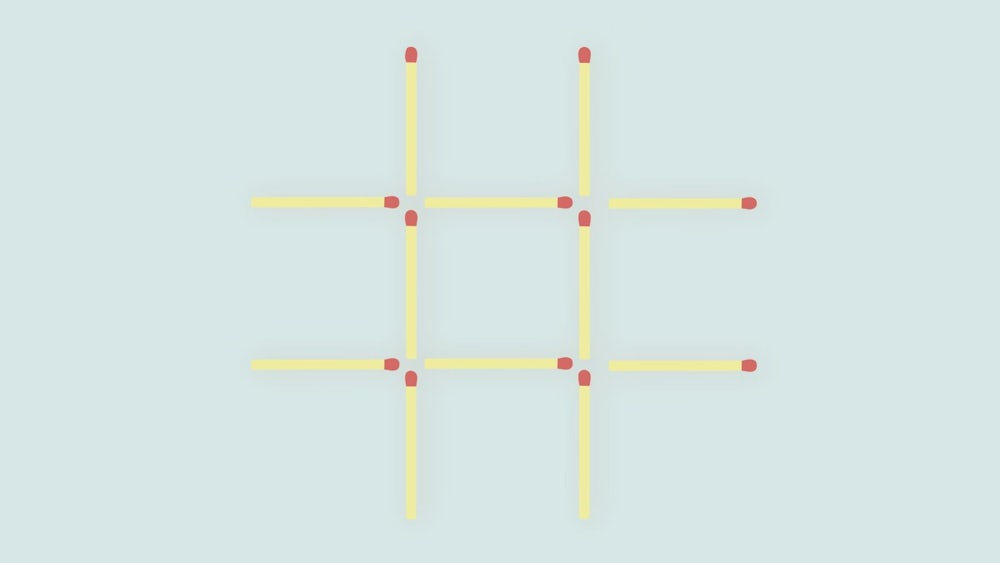
Das Rätsel der Woche Bauen Sie aus der Anordnung im Bild drei gleich große Quadrate, indem Sie genau drei Streichhölzer verschieben. Sie dürfen jedoch kein Hölzchen entfernen oder hinzufügen.
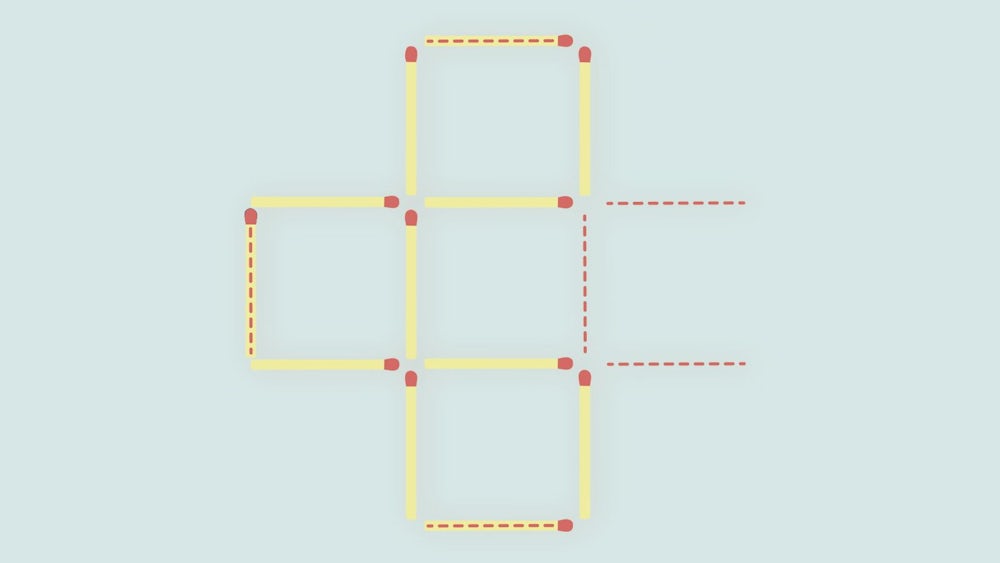
Die Lösung Liebe Streichholzverschieber, den vielen Mails mit korrekten Antworten nach zu urteilen, brauchen wir Ihnen diese Knobelei wohl nicht näher zu erklären. Daher belassen wir es gern bei der grafischen Lösung im Bild oben.

Das Rätsel der Woche Welche ist die kleinste ganze Zahl, die dem siebenfachen Wert der Summe ihrer einzelnen Ziffern entspricht?

Liebe Leser, mit ein bisschen Rumprobieren sind die meisten von Ihnen auf die korrekte Lösung gekommen. Dass es auch mathematisch-planvoll geht, zeigt unter anderem die Antwort von Mitspieler Ulrich L.: "Die gesuchte Zahl kann nicht einstellig sein. Annahme: Die gesuchte Zahl ist zweistellig mit a als Zehner- und b als Einerziffer. Also: 10a+b = 7(a+b) 10a+b = 7a+7b 3a = 6b a = 2b Dies eingesetzt in 10a+b ergibt 21b. Die gesuchte Zahl ist also 21." Dem haben wir nichts hinzuzufügen. Anmerkung: Einige Leser weisen uns darauf hin, dass auch die Null die Bedingung erfüllen würde. Da wir in der Aufgabe aber nach der kleinsten ganzen Zahl, "die dem siebenfachen Wert der Summe ihrer einzelnen Ziffern entspricht" gefragt haben, finden wir, dass eindeutig ist, dass nach einer aus mehreren Ziffern bestehenden Lösung gesucht ist.

Das Rätsel der Woche Sie stehen vor einem Raum und können nicht sehen, ob die im Raum hängende Glühbirne leuchtet. Außen befinden sich drei Lichtschalter, aber nur einer schaltet das Licht an. Sie möchten herausfinden, welcher Schalter der korrekte ist, dürfen den Raum aber nur ein einziges Mal betreten. Zu Beginn der Aufgabe ist die Glühbirne ausgeschaltet.
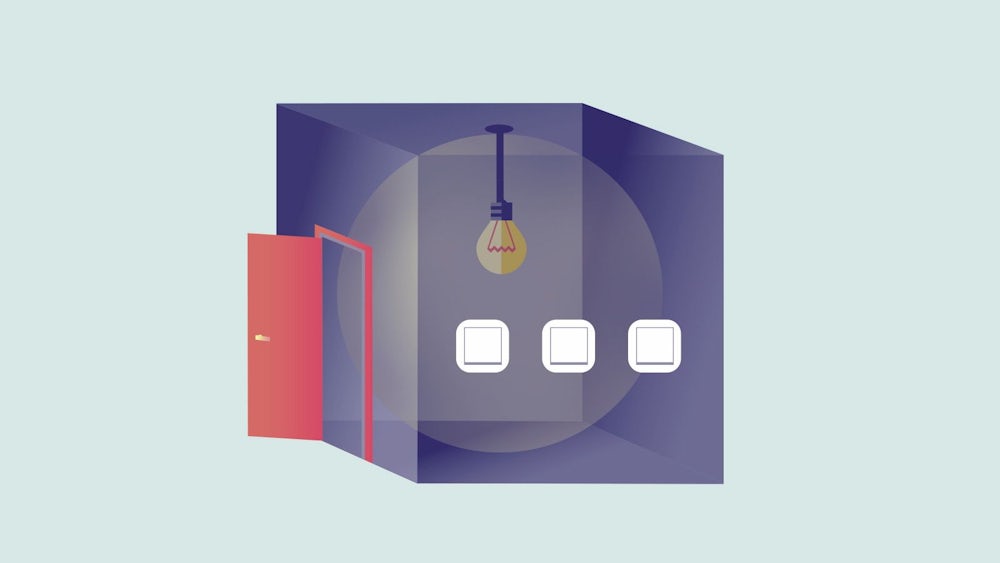
Die Lösung Liebe Leser, da ging den allermeisten von Ihnen zügig ein Licht auf. Drum wollen wir uns nicht lange aufhalten, Mitspieler Markus S. erklärt, wie es funktioniert: "Da nur die Anzahl, wie oft man den Raum betreten darf, nicht aber die Anzahl der Schalterbetätigungen begrenzt ist, kann man sich den recht schlechten Wirkungsgrad von Glühbirnen zunutze machen. Man betätigt zunächst einen Schalter und wartet einige Zeit. Anschließend betätigt man den Schalter erneut, legt daraufhin den nächsten Schalter um und betritt umgehend den Raum. Brennt die Lampe, hat man gerade eben den richtigen Schalter betätigt, ist die Lampe jedoch aus, muss man nur die Glühbirne anfassen und prüfen, ob sie warm ist (dann war der erste Schalter der richtige) oder kalt (dann ist der letzte verbliebene Schalter der richtige). Das Experiment funktioniert mit zunehmend effektiver arbeitenden Glühmitteln (z.B. LED) aber immer schlechter."
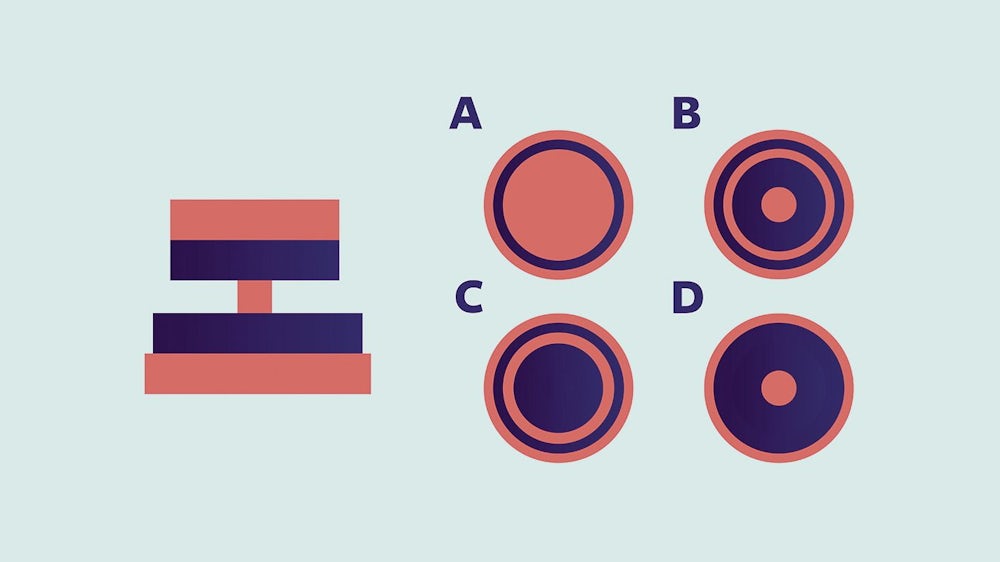
Das Rätsel der Woche Welche der Varianten A bis D ist die Vogelperspektive des Turmes auf der linken Seite?
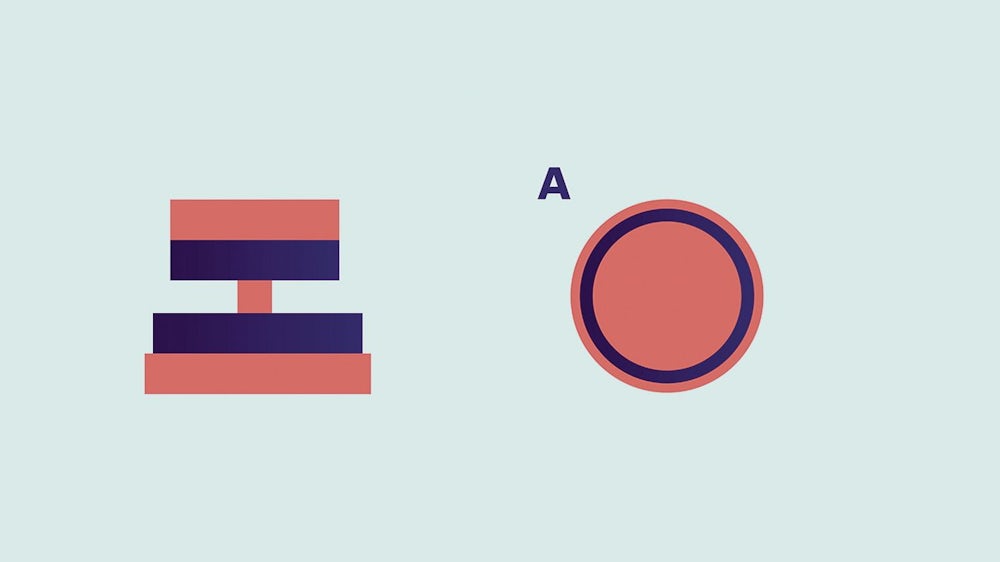
Liebe Leser, wieder mal haben wir Ihre Detailversessenheit unterschätzt. Sie dürfen grundsätzlich davon ausgehen, dass wir es nicht böse mit Ihnen meinen, und nicht mehr Fallstricke als nötig in unsere Rätsel einbauen. Also: Nein, die farbigen Flächen sind an der Oberseite nicht anders angemalt und auch nicht teils hohl. Und ja, das Verhältnis von Seiten- und Draufsicht des Turmes passt nicht ganz, dafür entschuldigen wir uns. Richtig ist natürlich Lösung A - und die lyrische Lösung von Stefan G. wollen wir Ihnen keinesfalls vorenthalten: "Ganz oben steh´ ich und blicke munter / von einem bunten Turm herunter. Egal ob Ost, ob West, ob Süd, ob Nord, für alle gilt, / der Blick nach unten zeigt stets das gleiche Bild. Dafür gibt´s wohl nur einen einz´gen Grund, / mir scheint, der schöne Turm, der ist rund. Dafür, es ist für das Rätsel nicht einerlei, / schöne Farben trägt er, zumindest zwei. Das Bild von oben, dem Himmel schon ganz nah, / schön anzusehen ist es und ich sag´ 'A'!"

Das Rätsel der Woche Die Hausnummer meines Bruders ist die Umkehrung meiner eigenen Hausnummer. Die Differenz der beiden Zahlen hat eine 2 am Ende. Welches ist das niedrigste Zahlenpaar, für das diese Angaben zutreffen?

Die Lösung Liebe Leser, haben Sie schon mal ein Haus mit der Nummer "08" gesehen? Wir auch nicht, deshalb lassen wir die Lösung 80/8 auch nicht gelten. Gelöst hat die Aufgabe zum Beispiel Mitspieler Stefan G.: "Zwischen den beiden Brüdern liegen 71 Häuser. Der eine Bruder wohnt in der Hausnummer 19, der andere in der 91 (Umkehrung). Die Differenz beträgt 72 oder -72, je nachdem, wie man es rechnet. Damit ist das die kleinste Paarung, die am Ende der Differenz eine 2 aufweist." Etwas kreativer ist Dirk S. an die Knobelei herangegangen: "Wie wäre es mit römischen Hausnummern? Dann ist das kleinste mögliche Paar 6 und 4, sprich IV und VI, Differenz ist 2." Well played, Herr S.! Wir wünschen Ihnen eine schöne Restwoche und freuen uns auf die nächste Knobelei.

Das Rätsel der Woche In der Dunkelheit des frühen Morgens wühlen Sie in Ihrer Sockenschublade: Dort befinden sich zehn weiße, zehn schwarze und zehn blaue Socken. Wie oft müssen Sie maximal einen einzelnen Socken herausziehen, um ein gleichfarbiges Paar zu haben? Zusatzaufgabe: Sollten Sie die Lösung zu dieser Knobelei schnell gefunden haben, wüssten wir auch noch gerne: Mit welcher Wahrscheinlichkeit ziehen Sie gleich bei den ersten beiden Versuchen zwei gleichfarbige Socken aus der Schublade?

Die Lösung Liebe Knobelfreunde, Sie haben diese doppelte Knobelei tapfer angenommen und und in den allermeisten Fällen auch gemeistert. Kommen wir direkt zur ersten Frage und der korrekten Antwort von Mitspieler Magnus J.: "Für die in der Aufgabenstellung genannte Situation braucht man maximal vier Versuche. Dann hat man zwei Socken von einer Farbe, welcher auch immer, in der Hand." Anders erklärt: Im ungünstigsten Fall ziehen Sie bei den ersten drei Versuchen einen Socken von jeder Farbe. Nach dem vierten Mal Ziehen haben Sie dann auf jeden Fall ein einfarbiges Paar zusammen. Bei der Zusatzaufgabe ist vielen von Ihnen möglicherweise der wenig geliebte Stochastikunterricht in der Schule in den Sinn gekommen. So funktionierts: Beim ersten Versuch können Sie nichts verkehrt machen, da wir keine spezielle Farbe angegeben haben, die aus der Schubalde gefischt werden soll. Die Wahrscheinlichkeit dafür, dass Sie irgendeinen Socken herausziehen, liegt also bei 1 bzw. 100 Prozent. Interessant wird es beim zweiten Versuch. In der Schublade sind noch 29 Socken - aber nur neun davon haben die gleiche Farbe wie der, den Sie bereits gezogen haben. Der Mathelehrer hätte nun darum gebeten, die günstigen den möglichen Fällen gegenüberzustellen. Will heißen: Die Wahrscheinlichkeit, dass sie einen Socken ziehen, der zu Ihrem ersten passt, liegt bei 9/29. Um die Wahrscheinlichkeit für das gesuchte Ergeinis zu bestimmen (zwei gleichfarbige Socken bei zwei Versuchen erwischen), müssen Sie nun bloß noch Wahrscheinlichkeit eins und zwei miteinander multiplizieren. Das ist in diesem Fall einfach: 1 * 9/29 = 9/29. Gerundet entspricht das ungefähr 31 Prozent.

Das Rätsel der Woche Na, finden Sie die Lösung?

Die Lösung Liebe Leser, mit diesem Rätsel verhält es sich wie mit dem Rest des Lebens auch: Es gibt viele Lösungen, und keine ist notwendigerweise besser oder schlechter als die andere. Was natürlich nicht heißt, dass man das eigene Ergebnis nicht amüsant erklären kann. So meint zum Beispiel Klaus G.: "Die Ergänzung ist offenkundig 13 zur Feier der glorreichen Idee, auf das Sozialgesetzbuch XIII zu verzichten. Nein, im Ernst. Eine einzige eindeutige Lösung gibt es nicht, lässt man beliebig komplexe Regeln zu. Auch die Ergänzung von 1, 2, 3, 4, 5, ? kann 11 lauten (1+2=3, 4+5=11). Der mit Zahlen befüllte Kreis besteht aus vier Segmenten (von links oben durchnummeriert mit 1 bis 4), wobei die Zahlen in den sich gegenüberliegenden Segmenten 1 und 3 addiert jeweils 21 ergeben. Die Segmentsumme von 4 ist 41. Dann müsste die Segmentsumme von Segment 2 ebenfalls 41 sein und die fehlende Zahl 22." Auf dieselbe Antwort kam auch Lisa D., sie erklärt sie aber anders: "Meine Lösung wäre die 22. Habe anfangs leider kein funktionierendes Schema erkennen können, also habe ich den Kreis waagrecht in zwei Stücke geteilt und die Summen beider berechnet. Damit diese gleich sind, habe ich das Fragezeichen durch die 22 ersetzt, sodass beide Summen 62 ergeben. Da sich dieses Schema wiederholt, wenn man den Kreis senkrecht teilt, hoffe ich, dass die Lösung stimmt." Den beiden Ansätzen haben wir nichts hinzuzufügen. Obwohl wir uns beim Erstellen des Rätsels eigentlich eine andere Variante ausgedacht hatten. Dafür wird der Kreis wie in der Erklärung von Klaus G. geviertelt. Unsere Lösung funktioniert dann nach dem Schema: Produkt der inneren beiden Ziffern/Zahlen plus Summe der äußeren beiden Ziffern/Zahlen liefert für alle Viertel das gleiche Ergebnis. Das bedeutet: 11 * 3 + (5 + 2) = 40 4 * 1 + (20 + 16) = 40 5 * 6 + (7 + 3) = 40 8 * 2 + (9 + ?) = 40 -> ? = 15 Alle weiteren Folgen aus unserer Reihe Knobelei der Woche finden Sie hier.