Es sieht alles ganz einfach aus auf dem Teufelsrad. Alle setzen sich auf die in der Mitte erhöhte Scheibe, diese beginnt sich zu drehen, sie beschleunigt auf 23 Umdrehungen pro Minute, und wer am längsten sitzen bleibt, gewinnt. Aber was entscheidet über Erfolg und Misserfolg? Worauf kommt es an? Ludwig Kugler, der Rekommandeur, sagt: vor allem auf die Kleidung. Wie dick oder dünn eine oder einer ist, sei egal. Wer gewinnen will, sollte einfach eine Lederhose tragen und lieber kein Dirndl. Schlecht seien auch Haferlschuhe oder Strumpfhosen, die seien "wie Glatteis". Besser stünden die Chancen mit Turnschuhen oder gleich ganz barfuß.
Stimmt das? Diese Frage ist wie geschaffen für Georg Eggers. Der Physiker lehrt an der Fakultät für angewandte Naturwissenschaften und Mechatronik an der Hochschule München, und in seiner Reihe "Physik des Scheiterns" erklärt er immer wieder bei Experimenten vor Publikum, warum ambitionierte Erfindungen in der Praxis dann doch nicht so gut funktioniert haben - vom selbstgebauten Billigflieger des Ikarus über die angeblich unsinkbare Titanic bis zum Weltraum-Telefon.
Hat Ludwig Kugler also Recht? In den Augen des Physikers ist das Teufelsrad ein flacher Kegel, der rotiert, auf dem also Zentrifugalkräfte wirken. Leider macht das Gefälle des Kegels die Formeln unübersichtlich. Deshalb erklärt Eggers alles erst einmal am Beispiel einer flachen Scheibe. Die Zusammenhänge sind dieselben.
Wichtig ist hier zunächst die Fliehkraft oder Zentrifugalkraft FZ, denn sie zieht die Gäste von der Scheibe. Die Kraft ergibt sich aus der Masse m des Gastes multipliziert mit der Winkelgeschwindigkeit w, mit der sich die Scheibe dreht, im Quadrat und dem Radius r, also der Entfernung des Gastes vom Mittelpunkt: FZ = m · w² · r. Je schneller sich also die Scheibe dreht und je weiter einer außen sitzt, desto stärker ist die Zentrifugalkraft. In der Mitte ist der Radius gleich null, und mit ihm die Fliehkraft. Dort ist also immer der beste Platz.
Um einen Gast ins Rutschen zu bringen, muss die Fliehkraft die Reibung überwinden
Doch die Formel besagt auch: Die Zentrifugalkraft wirkt umso stärker, je schwerer einer ist. Spielt das Gewicht also doch eine Rolle? Nein, sagt Eggers. Denn um einen Gast ins Rutschen zu bringen, muss die Fliehkraft erst einmal die Reibung überwinden, muss sie also größer sein als die sogenannte Haftreibungskraft: FZ > FR.
Diese Reibungskraft wiederum errechnet sich aus dem Reibungskoeffizienten µ, der von den gegeneinander reibenden Materialien abhängt, und aus der Normalenkraft FN; das ist diejenige Kraft, mit der ein Körper senkrecht auf die Unterlage drückt. Bei einer horizontalen Fläche ist FN identisch mit der Gewichtskraft FG. Und die erhält man, wenn man ihre Masse mit der Erdbeschleunigung g multipliziert. Die Formel lautet also: FR = FN · µ = m · g · µ. Damit aber steht bei der Ungleichung FZ >FR auf beiden Seiten die Masse m. Mit steigender Masse wachsen gleichermaßen die Zentrifugal- und die Reibungskraft. Und das heißt: Auf dem Teufelsrad ist es tatsächlich egal, wie viel einer wiegt.
Nun kommt die Steigung ins Spiel
Damit ist das Grundprinzip erklärt. Nun kommt die Steigung ins Spiel, und damit wird es komplizierter. An Körpern, die auf einer sich drehenden Scheibe hocken, zerrt nur die Fliehkraft. Auf einem rotierenden Kegel aber, also dem schrägen Teufelsrad, schiebt einen auch die Gewichtskraft in Richtung Rand. Darüber hinaus hebt einen ein Teil der Fliehkraft von der Oberfläche ab und vermindert so die Reibung. Auf dem Kegel ist es also gleich doppelt schwerer, sitzen zu bleiben.
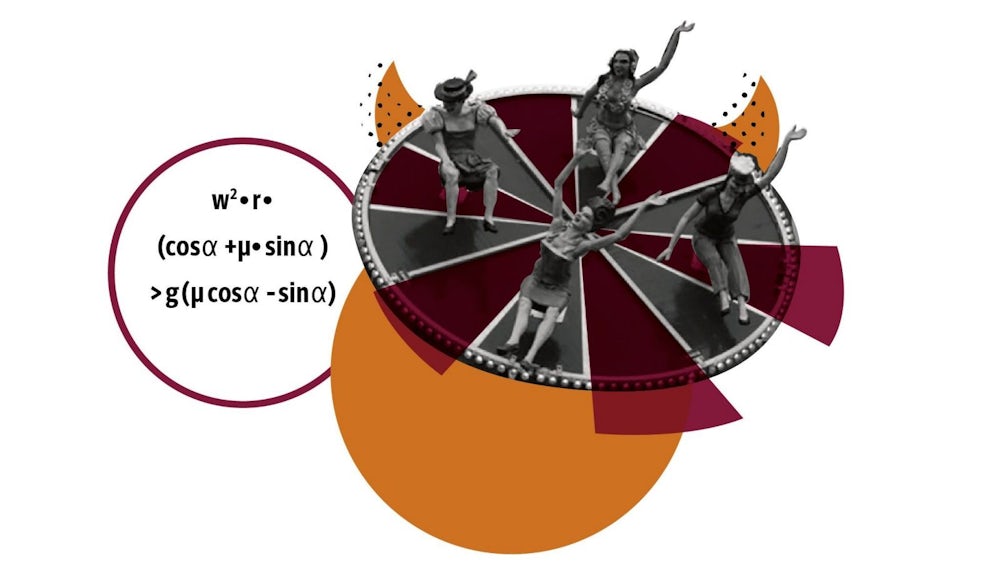
Um das physikalisch zu klären, müssen sowohl die Fliehkraft als auch die Gewichtskraft in Teilkräfte zerlegt werden, die parallel oder senkrecht zur Scheiben-Oberfläche wirken. Wie stark diese Teilkräfte sind, hängt vom Steigungswinkel Alpha des Kegels ab. Die Fahrt ist zu Ende, wenn die Gesamtkraft, die einen an den Rand zerrt, größer ist als die Reibungskraft auf der Schräge. Am Ende steht diese Ungleichung: w² · r · (µ · sin Alpha + cos Alpha)>g · (µ · cos Alpha - sin Alpha).

Der Rest ist Rechnen. Der Steigungswinkel des Teufelsrads ist klar: Die Scheibe misst fünf Meter im Durchmesser und ist in der Mitte um zwei Dezimeter erhöht, daraus ergibt sich ein Winkel von 4,6 Grad. Bleiben als Variablen die Drehgeschwindigkeit, der Radius und der ominöse Reibungskoeffizient. Der lässt sich schwer beschreiben, denn jede Lederhose ist anders - und auch unterschiedlich fettig. Hinzu kommt: Der Koeffizient ändert sich, wenn die Oberfläche nass wird. Wer schwitzt, der rutscht. Bier dagegen könne erst wie ein Schmiermittel wirken, beim Eintrocknen später aber kleben, sagt Eggers. Damit steige wiederum der Reibungskoeffizient.
Für Frauen im Dirndl hingegen wäre am gleichen Ort schon bei 3,8 Umdrehungen pro Minute Schluss
Für ein paar Beispielrechnungen sollen daher Näherungen genügen. Angenommen, eine Lederhose auf Holz hätte einen Reibungskoeffizienten in Höhe von 1 (das entspricht etwas mehr als dem Wert von Gummi auf Asphalt), ein Seidendirndl aber nur 0,1. Ein Lederhosenträger könnte sich dann ohne Weiteres auch auf halber Höhe des Teufelsrads hinsetzen, also bei einem Radius von 1,25 Metern. Von dort würde er erst bei einer Geschwindigkeit von 24,7 Umdrehungen pro Minute abrutschen. Im Normalbetrieb dreht sich das Teufelsrad aber nur mit 23 Umdrehungen pro Minute. Kein Wunder, dass die Betreiber regelmäßig mit Medizinbällen und Seilen nachhelfen müssen, um Menschen vom Teufelsrad zu befördern.
Für Frauen im Dirndl hingegen wäre am gleichen Ort schon bei 3,8 Umdrehungen pro Minute Schluss. Erfahrene Dirndlträgerinnen raffen auf dem Teufelsrad deshalb den Stoff und sitzen auf der nackten Haut. Wollte eine wirklich auf dem Kleid sitzen und bis zum Ende auf der Scheibe bleiben, müsste sie sich genau in die Mitte setzen, und zwar sehr genau. Bei 23 Umdrehungen pro Minute dürfte ihr Schwerpunkt maximal 3,4 Zentimeter vom Zentrum entfernt sein. Ein Millimeter mehr, und sie rutscht.
Zumindest theoretisch. Millimetergenau will sich Eggers dann doch nicht festlegen. Seine Disziplin zähle ja zu den Ingenieurwissenschaften, sagt er. Da würde er im Ernstfall nachhelfen, mit einem Vakuumsauger, einem Cyanacrylat-Klebstoff, einem Strahltriebwerk oder auch einer Holzschraube. Leider ist das auf dem Teufelsrad alles streng verboten.
In der Serie "Die Physik der Wiesn" analysiert die SZ in loser Folge verschiedene Bestandteile des Oktoberfests nach naturwissenschaftlichen Kriterien.
Gute Wiesn-Gschichten bleiben gut. Dieser Text wurde zuerst am 24. September 2018 veröffentlicht.